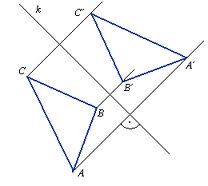
Symetria figur płaskich

O symetrii figur płaskich względem prostej mówi się prawidłowo, że jest to symetria względem osi symetrii.

Dwie figury nazywamy symetrycznymi do siebie względem danej osi, kiedy każdemu punktowi jednej figury odpowiada punkt drugiej figury, symetrycznie do niego względem tej osi położony. Jeśli dowolna figura płaska wygląda tak, że wszystkie jej punkty są parami symetrycznie położone względem pewnej prostej, to tę figurę nazywamy figurą symetryczną.

Składa się ona wtedy z dwóch części, symetrycznie do tej osi położonych względem siebie. Kiedy mamy figurę symetryczną do każdej wybranej to nazywamy ją wtedy obrazem symetrycznym, czyli obraz symetrii trójkąta względem osi to rójkąt do niego przystający.

O symetrii dwóch figur płaskich względem wybranego punktu mówimy, kiedy każdemu punktowi jednej figury odpowiada punkt drugiej figury, symetrycznie do niego względem tego punktu położony. Kiedy wybrana figura wygląda tak, że wszystkie jej punkty są parami symetrycznie położone względem pewnego punktu jako środka, to nazywamy tę figurę środkowo symetryczną.

I tak okrąg jest figurą symetryczną względem swego środka oraz obraz symetryczny prostokąta względem pewnego środka to prostokąt do niego przystający.