Twierdzenie Menelaosa

Wróćmy do starożytnej Grecji. Zajmiemy się teraz twierdzeniem Menelaos, które należy do dziedziny planimetrii.

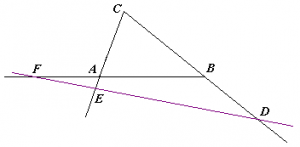
Jeżeli dowolna poprzeczna wyznacza na dwóch bokach trójkąta ABC i przedłużeniu trzeciego boku punkty D, E, F, to iloczyn trzech nieprzyległych do siebie powstałych w ten sposób odcinków jest równy długości trzech pozostałych odcinków. O wiele przejrzyściej wygląda to na wzorze:

|AE| x |CD| x |BF| = |BD| x |AF| x |CE|