Twierdzenie sinusów i cosinusów

Jeżeli twierdzenie Talesa wydaje się Wam skomplikowane, to teraz się trzymajcie. Przechodzimy do trygonometrii. Zaczniemy od twierdzenia sinusów (funkcje trygonometryczne wyrażają stosunki między bokami trójkąta względem miar jego kątów).

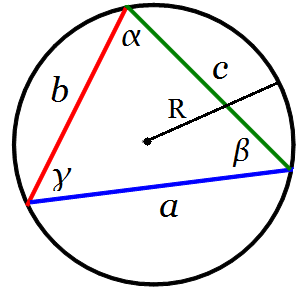
Twierdzenie sinusów mówi, że w dowolnym trójkącie iloraz długości dowolnego boku i sinusa kąta naprzeciw tego boku jest równy średnicy okręgu opisanego na tym trójkącie. Łatwiej wyrazić to wzorem:

a/sin α = b/sin β= c/sin γ = 2R.

Kolejnym twierdzeniem jest twierdzenie cosinusów. Mówi ono, że w dowolnym trójkącie kwadrat długości dowolnego boku jest równy sumie kwadratów długości pozostałych boków, pomniejszonej o podwójny iloczyn długości tych boków i cosinusa kąta zawartego miedzy nimi. W postaci wzoru wygląda to tak:

c² = a² + b² – 2ab cos γ.

Jeżeli weźmiemy za przykład trójkąt prostokątny, a kąt γ będzie kątem prostym to pojawi nam się zwykłe twierdzenie Pitagorasa, bowiem cosinus kąta prostego jest równy zeru.