Wzajemne położenie prostych

Wzajemne położenie prostych na płaszczyźnie to jedno z podstawowych pojęć w matematyce. Definicja tej sytuacji musi być znana już przez uczniów szkół podstawowych. Na zajęciach z geometrii rozpatrywane są dwa zjawiska matematyczne na płaszczyźnie: proste równoległe i proste prostopadłe. W pierwszym przypadku pozostają wobec siebie równoległe, nie przecinają się albo mogą się pokrywać . Natomiast w drugim proste mogą przecinać się wyłącznie w jednym punkcie.

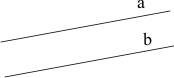
Proste równoległe

Pamiętać należy do proste równoległe, to takie proste, które znajdują się na jednej płaszczyźnie, ale nie mają żadnego punktu wspólnego. Wyróżnia się w tym wypadku także proste pokrywające się, czyli takie proste, których wszystkie punkty są wspólne. Można rzec, że dwie proste na płaszczyźnie są równoległe, wtedy kiedy ich współczynniki kierunkowe a są takie same.

Matematyczny zapis tej definicji wygląda następująco a ‖ b.

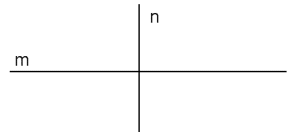
Proste prostopadłe

Natomiast proste przecinające się, to takie proste, które posiadają dokładnie jeden punkt wspólny. Wyróżnia się szczególny przypadek prostych przecinających się. Są to proste prostopadłe, czyli ich kąt przecięcia wynosi dokładnie 90 stopni. W tym przypadku współczynnik kierunkowy jednej prostej musi być odwrotnością drugiego współczynnika kierunkowego.

W matematyce tę sytuację zapisuje się jako a ± b.